AERO ODYSSEY
Newtonian Orbital Mechanics: Moon and Satellite orbiting Earth
Introduction
I decided to first start out with a basic Newtonian mechanical problem to ease into numerical simulation of a real physical problem. I wanted to test the ability of a basic level numerical iteration technique on a high school/ freshman college level physics problem. I solve this problem utilizing MATLAB however, almost any programming language can be used to solve this. So if you are comfortable with python, C and so on, I encourage you to extrapolate from this tutorial.
I utilized an Euler iteration technique to simulate the orbit of the moon around earth and simultaneously a satellite around the moon. Before you freak out, I will say this problem is surprisingly easy assuming you have a basic physics based background and some coding experience. Pleasantly (or maybe not so pleasantly) this problem actually presents how earth’s orbit is dependent on each other planetary body. Between numerical errors and neglecting other orbiting bodies we get close to the exact orbit shape of earth but not exact.
Mathematical Background
Before we get into the programming let me lay out the mathematical/physical ground work we will program into MATLAB. Below is my initial positions of the earth, moon and satellite (sat) labeled as I annotated in my MATLAB program.

Earth, moon and satellite diagram. R stands for the radius between orbital bodies and “V” stands for the velocity vector at the very beginning of the simulation. If we act as “God”, we would start the bodies in this position with the velocities of the bodies going in the annotated directions.
R stands for the radius between the orbital bodies. Speaking in Cartesian coordinates, center of earth is the 0,0 point in a 2D plane. Please contact me if the visual is not clear however I think this is self explanatory. Now getting into the orbital mechanics of the orbiting bodies. We first start out with the governing equation:
This states that the Force applied by body one onto body two is a function of the gravitational constant and the distance squared between the two bodies. Inspecting this equation one can see that the force becomes stronger as the two bodies approach one another.
This is the primary governing equation to determine the motion of the bodies. Yes its almost that simple. The rest of the information is recalling what force is and how to derive the position by knowing the acceleration (high school physics). Not to diminish the possible difficulty that lays ahead, but the fundamentals are as simple as seen by the equation above. Remember the following equations will provide the driving framework for the MATLAB code that was developed.
Recalling that force is a function of mass and acceleration and that acceleration is the integral of velocity, one can develop some equations utilizing our force equation to obtain the velocity of the orbital bodies.
Now remember that Newton's gravitational law states that the force from body one is applied to body two. Thus F = the force applied onto body two caused by body one. This means if we know the force we can determine the acceleration of body two. If we know the mass of the earth, moon and the distance between the two, we know the force! If we know the force we can calculate the acceleration and subsequently we can integrate and determine the velocity and similarly the position of body two at the start of the system! this is the basic fundamentals of the Euler iteration by incorporating Newton's gravitational equation. Exciting stuff!
If you have no background in numerical analysis I recommending you at least familiarizing yourself with it before proceeding. Although I brake it down the best I can, if you do not have any background it may be tough to grasp. However, I encourage you to read a head and see if you can pick it up. Euler numerical integration is a very simple way to integrate a value that is only dependent on a single variable. In our case our velocity is dependent on time. Thus we integrate with respect to time. Numerically speaking our time is discretized into desired time steps. This means we want to determine how much our velocity and thus our position has changed between step n and step n+1. If we use a very small time step (dt) the more refine our change in velocity and position will be and much more accurate as opposed to a larger d. The smaller time step comes at a cost. The cost is computational effort from the computer. A smaller time step, say dt = 0.001s requires many more iterations to calculate the same distance then say dt = 1s. dt is chosen at the discretion of the programmer, however in different numerical integration techniques there are guidelines and rules that could help provide a stable solution but for this it comes down to how fine do we need our change in position.
Remember we are talking planets here. It takes the moon about 27 days to orbit the earth. The distance and time scale is huge compared to some problems, thus our dt does not need to be 0.001s. In my matlab program i brake our integration up into two seperate time steps. One for our satellite respect to the moon and for the moon with respect to earth. Since it takes less time for the sattelite (sat) to orbit the moon than the moon to orbit earth we need a more refined time step for the sat, thus our dt for the sat is about 600s and for the moon orbiting the earth its about 3600s. These numbers where chosen for my computers ability to process the amount of data and still give an accurate answer.
Enough about the theory and boring stuff. lets get into the equations. Below are the generalized quations for the Euler integration that we will apply to equations above.
The following paragraphs are in the context of the earth applying a force to the moon and or sat. First F is calculated by utilizing the mass of the moon/sat and the earth (m1) and the distance between them. Then a is calculated by dividing m2 over. This is the force of the earth onto the other body. We have to get into some basic vector math (I'm sorry). Since we are operating in a 2D world our force, acceleration (a), velocity (v) and position (r) have two components, x and y directions. Because of this we create two arrays and track the acceleration, velocity and position in both the x and y directions. This will become more clear once you review the code. Ignoring the 2D effects for now, the velocity is calculated above based off the force applied, acceleration calculated from the force and the pre determined time step size then added to the previous velocity (what your velocity is currently). This newly calculated velocity is the velocity after dt seconds elapse. Similarly for the position.
Determining the x and y components of the vectors for acceleration, velocity and position does not add much work to the math. If you have a little bit of programming background its implementation is relatively simple. Below is a few key relationships for vector math which is needed. Remember in Newton's gravitational force equation there is the distance between the bodies? well the r variable is really the x and y distance from the center from body one. Thus we need the relative direction components. Thus r from earth to the moon is:
These are the x and y position components respectively that will be used to calculated the force that is applied in the x and y directions and thus the acceleration, velocity and ultimately the position in x and y cartesian coordinates.
With this ground work laid out I hope the following code layout will make sense. Remember the code is posted in MATLAB format. If you have questions regarding the code breakdown please reach out and ask. If the background is not clear please reach out and ask.
MATLAB CODE
First we start out with decaring our masses, initial positions of orbital bodies, velocities and accelerations to then calculate the inital forces applied by all bodies to each other. Many of these conditions can be found with a simple google search. Lets assume we start with everything at appogee with respect to earth. We can then find the distance of the moon and velocity with respect to earth. This is given by NASA. Easy as that! Good thing they did the work for us. Using this information we can then set up the first part the code which is listed below.
%% Thre Body Problem
clear all
clc
close all
%constants
R1=6356; % radius of earth km
M1=5.9724*10^24 % (kg) mass of earth 5.6722*10^24
G=6.67408*10^-11/1000^3 % gravitational constant km^3/kg*s^2 6.67408*10^-11
M2=0.07346*10^24; %mass of moon (kg)
R2=R1/3.674; %km
%Create earth and moon
%plot(earthx,earthy,moonx,moony)
%starting position vector and velocity
v1=[0,0,0]; %velocity of earth for all tense and purposes is zero relative to the moon
v2=[0,0.97,0]; %velocity of moon relative to earth at appogee (0.97km/s)
pos2=[0.4055*10^6,0,0];
pos1=[0,0,0];
%time
dt=3600 %calculate once every hr
t=0;
dtsat=600;
tsat=0;
%now add satelite around moon
M3=4424; %kg sat
v=sqrt(G*M2/(R2+3000));
pos3=[(0.4055*10^6)-3000,0,0];
v3=[0,v+0.97,0];
Most of the values above were pulled from online from sites built my NASA linked at the button below:
The R2 radius may look weird however that is the ratio of the moon normalized by the distance of the earth to the moon. This was just me messing around and not finishing my generalization of my code. R2 could easily just be the radius of the moon. Investigating v1 we can see that the x, y and z values are all 0. this is because we want the earth to be our center frame of reference. Thus everything is moving about the earth same for pos1. v2 is the velocity of the moon when we let our simulation begin. The moon at apogee is moving only in the y direction at 0.97km/s relative to earth, looking top down. Now v3 is a bit tricky. using v we calculate the velocity of the satellite at 3000km above the moon then relate that speed to what it would appear on earth. the equation for v can be found Wikipedia however its given in the code above. Once again. If this doesn't make sense please reach out and ask or let me know. Now stepping into the Euler integration we have two loops. One calculating every 600s and the other storing the values every 3600s. Remember these values from above? This was chosen to reduce the computational time of plotting. In MATLAB much of the resources to create an animation is dedicated to plotting. The mathematical calculations are about 10% of the overall time.
frame=1;
i=1;
%plotting info
j=1;
m=1;
while t<(27.3217*24*60*60)*1 %27.32 days in sec
count=1;
while tsat<3600
r32=pos2-pos3;
r12=pos2-pos1;
r31=pos3-pos1;
F21=-G*M1*M2.*(r12/norm(r12))/norm(r12).^2;
F12=-F21;
a1=F12./M1;
v1=v1+a1*dtsat;
a2=F21./M2;
v2=v2+a2*dtsat;
pos1=pos1+v1*dtsat;%[0,0,0];%pos1+v1*dt;
pos2=pos2+v2*dtsat;
moonx(i)=pos2(1);
moony(i)=pos2(2);
%plotpos2(count)=pos2
F31=G*M3*M2.*(r31/norm(r31))/norm(r31).^2;
F32=G*M3*M2.*(r32/norm(r32))/norm(r32).^2;
a3=(F31+F32)./M3;
v3=v3+a3*dtsat;
pos3=pos3+v3*dtsat;
tsat=tsat+dtsat;
if j>=2
moonx1(m)=pos2(1);
moony1(m)=pos2(2);
pos3plotx(m)=pos3(1);
pos3ploty(m)=pos3(2);
j=1;
m=m+1;
end
j=j+1;
i=i+1;
count=count+1;
end
earthx=pos1(1);
earthy=pos1(1);
moonx=pos2(1);
moony=pos2(2);
satx=pos3(1);
saty=pos3(2);
t=t+dt;
tsat=0;
end
Reviewing the code above you can clearly see all the elements covered above. I am integrating down to position then storing that info every loop. Then I update the position after I exit the inner most while loop. The outer most while loop iterates for the total amount of time it takes the moon to orbit the earth once (in earth days). There are a few items in this code that can be refined and removed however it works well enough. I may later optimize this code but it gets the point across well enough I think. If not please let me know and of course utilize and modify this code as you feel fit. The last mid of this code is more MATLAB specific to make my plots and videos for some fun animations to show off. this is not necessary however this has not point if you can visualize it!
video=VideoWriter('earthmoonandsat1.mp4','MPEG-4');
video.FrameRate=20;
%video.CompressionRatio=15;
open(video)
figure('Renderer', 'painters', 'Position', [900 100 1200 1200])
%plot(0,0,'x')
for i=1:300%length(moonx1)
%delete(gca)
p=plot(0,0,'x',moonx1(i),moony1(i),'.',pos3plotx(i),pos3ploty(i),'.');
axis([-0.4255*10^6,0.4255*10^6,-0.4255*10^6,0.4255*10^6]);
h=gca;
get(h,'FontSize') ;
set(h,'FontSize',5);
xlabel('X (km)','fontSize',12);
ylabel('Y (km)','fontSize',12);
title('moon orbiting earth with satellite','fontsize',12);
p(2).MarkerSize=10;
p(3).MarkerSize=6;
axis([-0.4255*10^6,0.4255*10^6,-0.4255*10^6,0.4255*10^6]);
M=getframe(gca);
writeVideo(video,M)
%delete(gca)
end
close(video);
The previous code produces the following image and video. The image below is a zoomed in on the hysteresis path of the sat orbiting the moon as they both orbit the moon in the frame of reference of the earth. The video is a "real" time video of a path of the simulation to show the orbits around earth. The image and video give a neat perspective of the Apollo module orbiting while men walked on the moon! If you want, you can look at the perigee for the moon (exact opposite x position of the starting position of the simulation) and see that it is less then 1% off from the reported number by NASA! That is pretty remarkable.
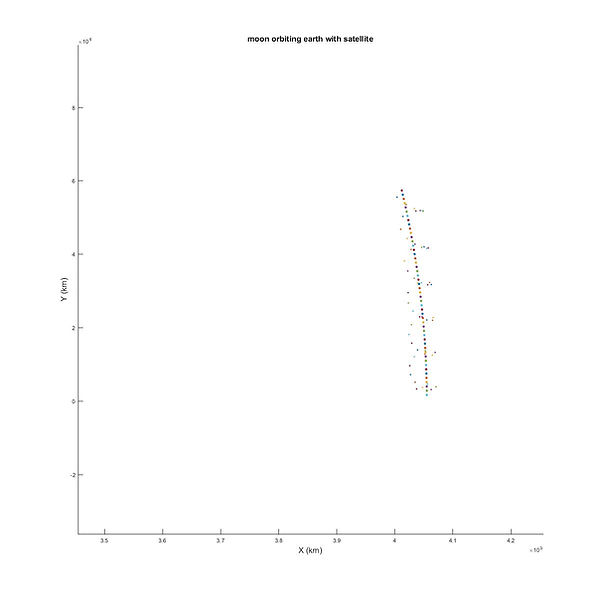
If you have made it this far then congrats! This example just shows the power of numerical analysis, computers and the power of even the most basic physical theories that have been around for years! I am still new to all of this so if you would like to see more detail in certain areas or if something is not clear please reach out and let me know! There are many good tutorials out there on stuff like this but my goal is when i get into more difficult examples I will be able to provide a more simplified and for a lack of a better term, dumbed down approach that is easier to understand then those who feel its necessary to present info in a conveluted way.